Wine.B.Cellarの定理

上の図をご存知だろうか。Wine.B.Cellarのパラドックスといわれる図である。
同じ図形を使っているのに面積に違いが生まれているのがお分かりだろう。
この図形を発見したCellar氏は研究を重ね「幾何学において得られる結果は、さまざまなありようの中の一つの可能性に過ぎない」というWine.B.Cellarの定理を発表しこれによって2006年にノーベル幾何学賞を受賞している。
この後さまざまな人がWine.B.Cellarのパラドックス図形を発見し、今では幾何学の計算などによって求められる結果には最大5%程度の誤差が生まれる可能性がある、というのが数学者においての常識となりつつある。
しかし、ここからが問題なのだが、中学や高校の数学にこの定理を適用するかどうかが問題となっており今の段階で見送られている状況。数学教師の中にはこの定理を知らないものもいるようで、数学好きの生徒に詰め寄られて困惑するということも頻発しているようだ。
というのはもちろん嘘で(完全にでっちあげです)、上の図はこの記事からの転載。この絵をみて一瞬ありえないと思ったのですが、ありえないことがあるはずがないと思ってしばらく考えてしまいました。そんな中ありえないことがありえたんだったら面白いなぁと思う自分もいたり。
例えば学校の幾何学のテストで微妙な数字の違いで間違えたときに、この記事の上の部分だけプリントして「先生、これってWine.B.Cellarの定理による誤差の範囲内だから正解じゃないっすかぁ?」と数学教師に突きつけてみたらどういう反応が返ってくるだろうか。
その反応でその教師が数学をどれだけ愛しているのか、どのように愛しているのかが分かるかもしれません。(鼻で笑われるかもしれませんが・・・)
 MEMO「壁」
MEMO「壁」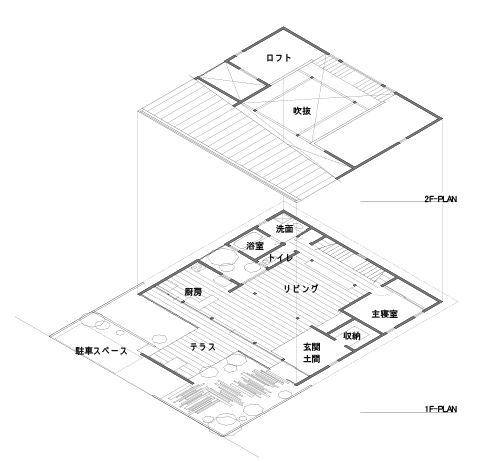 HS-05 低姿勢の家
HS-05 低姿勢の家
 出会う建築
出会う建築 動態再起論
動態再起論 環境配慮型ブランド
環境配慮型ブランド 不動産
不動産